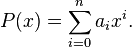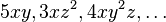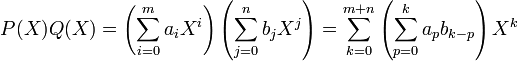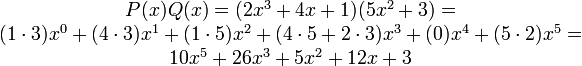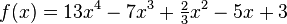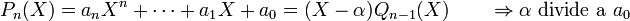En el presente bloque se pretende que el alumno:
1.- Desarrolle la habilidad de construir modelos aritméticos y algebráicos aplicando las propiedades de los números reales, con la finalidad de resolver problemas de su contexto.
2.-Identifique las caracteristicas presentes en tablas, gráficas, mapas, diagramas y textos, provenientes de situaciones cotidianas para traducirlas en lenguaje aritmético o algebráico.
COMENTARIOS DE LOS LECTORES
miércoles, 19 de octubre de 2011
BLOQUE 3: Sumas y Sucesiones de Números
Una sumatoria de números reales es una suma de ciertos números que mantienen una relación entre si. La sumatoria de una serie de números es la suma desde el primero hasta el n-simo número de una colección, asi por ejemplo; la sumatoria de los primeros cinco números natuarales impares es 1+3+5+7+9=25.
El creador de la teoría de las series y sucesiones fue el matemático francés Pierre de Fermat.
Las sucesiones son colecciones de números reales que mantienen un orden y relación que puede ser de tipo algebraica o de tipo geométrica.
El creador de la teoría de las series y sucesiones fue el matemático francés Pierre de Fermat.
Las sucesiones son colecciones de números reales que mantienen un orden y relación que puede ser de tipo algebraica o de tipo geométrica.
BLOQUE 9: RESOLUCION DE SISTEMAS DE ECUACIONES DE 3 ECUACIONES LINEALES CON TRES VARIABLES
Este es el método de resolución por el método de Cramer:
BLOQUE 9: ECUACIONES CUADRÁTICAS
En este bloque estudiaremos la resolución de la ecuación de segundo grado, para lo cual existen diferentes métodos. A continuación trataremos del método de resolución por medio de la ecuación general de 2° grado:
jueves, 13 de octubre de 2011
BLOQUE 7: ECUACIONES LINEALES II
Fundamentalmente trataremos la resolución de sistemas de ecuaciones lineales con vos variables. Un ejemplo lo tenemos en el siguiente video:
BLOQUE 5: TRANSFORMACIONES ALGEBRAICAS
De manera suscinta trataremos cómo factorizar trinomios de diversos tipos, obtener factores comunes,dividir polinomios, representaciones simbólicas o gráficas y aplicaciones a modelos matemáticos.
miércoles, 12 de octubre de 2011
BLOQUE IV: Transformaciones Algebráicas
Las transformaciones algebráicas se refieren a todo tipo de operaciones que involucran expresiones algebraicas.
Polinomio
De Wikipedia, la enciclopedia libre
(Redirigido desde Polinomios)
Saltar a: navegación, búsqueda
En matemáticas , se le llama polinomio a la suma de varios monomios. Un monomio es un producto de un coeficiente y una variable elevado a un número natural, que se llama el exponente del monomio.
Ejemplos de monomios son . El siguiente ejemplo describe en detalle las partes de un monomio. Si consideramos el monomio:
. El siguiente ejemplo describe en detalle las partes de un monomio. Si consideramos el monomio:
El grado de un monomio es su exponente. El grado de un polinomio es el del monomio de mayor grado. En el polinomio, existe el término independiente, que es un monomio que no tiene parte literal o variable, es decir, que no tiene variables o letras que lo acompañen. Algunos ejemplos:
 . En particular los números (o elementos del anillo
. En particular los números (o elementos del anillo  ) son polinomios de grado cero.
) son polinomios de grado cero.
 o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma
 es un momonio de tres variables (ya que en él aparecen tres letras x, y y z), el coeficientes es 4, y los exponentes son 1, 2 y 1, ya que xy2z = x1y2z1.
es un momonio de tres variables (ya que en él aparecen tres letras x, y y z), el coeficientes es 4, y los exponentes son 1, 2 y 1, ya que xy2z = x1y2z1.
 y
y  y el polinomio producto
y el polinomio producto  :
:
 (junto con la operación
(junto con la operación  ) por lo que la expresión (*) puede extenderse también al caso de que alguno de los polinomios sea nulos.
) por lo que la expresión (*) puede extenderse también al caso de que alguno de los polinomios sea nulos.
Debido a su estructura simple, las funciones polinómicas son muy sencillos de evaluar numéricamente, y se usan ampliamente en análisis numérico para interpolación polinómica o para integrar numéricamente funciones más complejas. Una manera muy eficiente para evaluar polinomios es la utilización de la regla de Horner.
En álgebra lineal el polinomio característico de una matriz cuadrada codifica muchas propiedades importantes de la matriz. En teoría de los grafos el polinomio cromático de un grafo codifica las distintas maneras de colorear los vértices del grafo usando x colores.
Con el desarrollo de la computadora, los polinomios han sido remplazados por funciones spline en muchas áreas del análisis numérico. Las splines se definen a partir de polinomios y tienen mayor flexibilidad que los polinomios ordinarios cuando definen funciones simples y suaves. Éstas son usadas en la interpolación spline y en gráficos por computadora.
La función
En un anillo conmutativo una condición necesaria para que un monomio sea un factor de un polinomio de grado n > 1, es que el término independiente del polinomio sea divisible por la raíz del monomio:
una condición necesaria para que un monomio sea un factor de un polinomio de grado n > 1, es que el término independiente del polinomio sea divisible por la raíz del monomio:
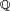 pero sí factoriza sobre
pero sí factoriza sobre  :
:
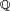 , ni tampoco sobre
, ni tampoco sobre  aunque factoriza sobre
aunque factoriza sobre  :
:
En el problema 14º del papiro de Moscú (ca. 1890 a. C.) se pide calcular el volumen de un tronco de pirámide cuadrangular. El escriba expone los pasos: eleva al cuadrado 2 y 4, multiplica 2 por 4, suma los anteriores resultados y multiplícalo por un tercio de 6 (h); finaliza diciendo: «ves, es 56, lo has calculado correctamente». En notación algebraica actual sería: V = h (t² + b² + tb) / 3, un polinomio de cuatro variables (V, h, t, b) que, conociendo tres, permite obtener la cuarta variable.
Algunos polinomios, como f(x) = x² + 1, no tienen ninguna raíz que sea número real. Sin embargo, si el conjunto de las raíces posibles se extiende a los números complejos, todo polinomio (no constante) tiene una raíz: ese es el enunciado del teorema fundamental del álgebra.
Hay una diferencia entre la aproximación de raíces y el descubrimiento de fórmulas concretas para ellas. Se conocen fórmulas de polinomios de hasta cuarto grado desde el siglo XVI (ver ecuación cuadrática, Gerolamo Cardano, Niccolo Fontana Tartaglia). Pero, las fórmulas para polinomios de quinto grado fueron irresolubles para los investigadores durante mucho tiempo. En 1824, Niels Henrik Abel demostró que no puede haber fórmulas generales para los polinomios de quinto grado o mayores (ver el teorema de Abel-Ruffini). Este resultado marcó el comienzo de la teoría de Galois que se ocupa del estudio detallado de las relaciones existentes entre las raíces de los polinomios.
La máquina diferencial de Charles Babbage fue diseñada para crear automáticamente tablas de valores de funciones logarítmicas y diferenciales, evaluando aproximaciones polinómicas en muchos puntos, usando el método de las diferencias de Newton.
Ejemplos de monomios son
 . El siguiente ejemplo describe en detalle las partes de un monomio. Si consideramos el monomio:
. El siguiente ejemplo describe en detalle las partes de un monomio. Si consideramos el monomio:es un monomio con coeficiente 6, variable x y exponente 5. Por tanto, el grado de este monomio es 5.
El grado de un monomio es su exponente. El grado de un polinomio es el del monomio de mayor grado. En el polinomio, existe el término independiente, que es un monomio que no tiene parte literal o variable, es decir, que no tiene variables o letras que lo acompañen. Algunos ejemplos:
- P(x) = 2, polinomio de grado cero.
- P(x) = 3x + 2, polinomio de grado uno.
- P(x) = 2x2+ 3x + 2, polinomio de grado dos.
 . En particular los números (o elementos del anillo
. En particular los números (o elementos del anillo  ) son polinomios de grado cero.
) son polinomios de grado cero.Contenido[ocultar] |
[editar] Definición algebraica
[editar] Polinomios de una variable
Para a0, …, an constantes en algún anillo (en particular podemos tomar un cuerpo, como o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la formaEl polinomio se puede escribir más concisamente usando sumatorios como
[editar] Polinomios de varias variables
Los polinomios de varias variables son similares a los de una variable. La diferencia es que en ellos cada uno de los monomios puede contener más de una letra de variable. Por ejemplo:Son monomios de varias variables. Más en detalle el último de ellos
 es un momonio de tres variables (ya que en él aparecen tres letras x, y y z), el coeficientes es 4, y los exponentes son 1, 2 y 1, ya que xy2z = x1y2z1.
es un momonio de tres variables (ya que en él aparecen tres letras x, y y z), el coeficientes es 4, y los exponentes son 1, 2 y 1, ya que xy2z = x1y2z1.[editar] Operaciones con polinomios
Artículo principal: Operaciones con polinomios
Los polinomios se pueden sumar y restar agrupando los términos y simplificando los monomios semejantes. Para multiplicar polinomios se multiplica cada término de un polinomio por los términos del otro polinomio y se simplifican los monomios semejantes, posteriormente. Por ejemplo:Para poder realizar eficazmente la operación tienes que adquirir los datos necesarios de mayor a menor. Una fórmula analítica que expresa el producto de dos polinomios es la siguiente:
Aplicando esta fórmula al ejemplo anterior se tiene:
Puede comprobarse que para polinomios no nulos se satisface la siguiente relación entre el grado de los polinomios
 y
y  y el polinomio producto
y el polinomio producto  :
:(*)Puesto que el producto de cualquier polinomio por el polinomio nulo es el propio polinomio nulo, se define convencionalmente que
 (junto con la operación
(junto con la operación  ) por lo que la expresión (*) puede extenderse también al caso de que alguno de los polinomios sea nulos.
) por lo que la expresión (*) puede extenderse también al caso de que alguno de los polinomios sea nulos.[editar] Funciones polinómicas
Artículo principal: Función polinómica
Las funciones polinómicas son funciones que se basan en expresiones de tipo polinomio. Una función polinómica puede definirse como la operación resultante de substituir la letra x en un polinimo en esa variable por un número. La funciones polinómicas reales son funciones suaves, esto es, son infinitamente diferenciables (tienen derivadas de todos los órdenes finitos).Debido a su estructura simple, las funciones polinómicas son muy sencillos de evaluar numéricamente, y se usan ampliamente en análisis numérico para interpolación polinómica o para integrar numéricamente funciones más complejas. Una manera muy eficiente para evaluar polinomios es la utilización de la regla de Horner.
En álgebra lineal el polinomio característico de una matriz cuadrada codifica muchas propiedades importantes de la matriz. En teoría de los grafos el polinomio cromático de un grafo codifica las distintas maneras de colorear los vértices del grafo usando x colores.
Con el desarrollo de la computadora, los polinomios han sido remplazados por funciones spline en muchas áreas del análisis numérico. Las splines se definen a partir de polinomios y tienen mayor flexibilidad que los polinomios ordinarios cuando definen funciones simples y suaves. Éstas son usadas en la interpolación spline y en gráficos por computadora.
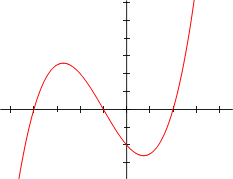
[editar] Ejemplos de funciones polinómicas
Note que las gráficas representan a las funciones polinomiales y no a los polinomios en sí, pues como se dice define anteriormente, un polinomio es la suma de varios monomios.[editar] Factorización de polinomios
Artículo principal: Factorización
Para factorizar un polinomio de segundo grado completo (con todos los términos) se divide por el inverso de una de sus raíces sumado con la incógnita, siendo los factores el número por el que dividimos y el resultado; ya que no hay resto, cumpliéndose así que dividendo = incógnita - divisor Χ cociente + resto, siendo este el resultado final hayado para completar la ecuación. En caso de que el polinomio no tenga término independiente se sacará la incógnita como factor común y ya está factorizado. También se puede factorizar usando las igualdades notables.En un anillo conmutativo
 una condición necesaria para que un monomio sea un factor de un polinomio de grado n > 1, es que el término independiente del polinomio sea divisible por la raíz del monomio:
una condición necesaria para que un monomio sea un factor de un polinomio de grado n > 1, es que el término independiente del polinomio sea divisible por la raíz del monomio:Debe tenerse presente que el que un polinomio factorice o no depende de sobre qué anillos se considere la factorización, por ejemplo el polinomio X2-2 no factoriza sobre
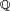 pero sí factoriza sobre
pero sí factoriza sobre  :
:Por otra parte X2+2 no factoriza ni sobre
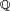 , ni tampoco sobre
, ni tampoco sobre  aunque factoriza sobre
aunque factoriza sobre  :
:Un cuerpo en el que todo polinomio no constante factoriza en monomios es un cuerpo algebraicamente cerrado.
[editar] Historia
La resolución de ecuaciones algebraicas, o la determinación de las raíces de polinomios, está entre los problemas más antiguos de la matemática. Sin embargo, la elegante y práctica notación que utilizamos actualmente se desarrolló a partir del siglo XV.En el problema 14º del papiro de Moscú (ca. 1890 a. C.) se pide calcular el volumen de un tronco de pirámide cuadrangular. El escriba expone los pasos: eleva al cuadrado 2 y 4, multiplica 2 por 4, suma los anteriores resultados y multiplícalo por un tercio de 6 (h); finaliza diciendo: «ves, es 56, lo has calculado correctamente». En notación algebraica actual sería: V = h (t² + b² + tb) / 3, un polinomio de cuatro variables (V, h, t, b) que, conociendo tres, permite obtener la cuarta variable.
Algunos polinomios, como f(x) = x² + 1, no tienen ninguna raíz que sea número real. Sin embargo, si el conjunto de las raíces posibles se extiende a los números complejos, todo polinomio (no constante) tiene una raíz: ese es el enunciado del teorema fundamental del álgebra.
Hay una diferencia entre la aproximación de raíces y el descubrimiento de fórmulas concretas para ellas. Se conocen fórmulas de polinomios de hasta cuarto grado desde el siglo XVI (ver ecuación cuadrática, Gerolamo Cardano, Niccolo Fontana Tartaglia). Pero, las fórmulas para polinomios de quinto grado fueron irresolubles para los investigadores durante mucho tiempo. En 1824, Niels Henrik Abel demostró que no puede haber fórmulas generales para los polinomios de quinto grado o mayores (ver el teorema de Abel-Ruffini). Este resultado marcó el comienzo de la teoría de Galois que se ocupa del estudio detallado de las relaciones existentes entre las raíces de los polinomios.
La máquina diferencial de Charles Babbage fue diseñada para crear automáticamente tablas de valores de funciones logarítmicas y diferenciales, evaluando aproximaciones polinómicas en muchos puntos, usando el método de las diferencias de Newton.
[editar] Véase también
- Operaciones con polinomios
- Teorema del resto
- Factorización
- Álgebra
- Álgebra elemental
- Teorema fundamental del álgebra
[editar] Enlaces externos
 Wikimedia Commons alberga contenido multimedia sobre PolinomioCommons
Wikimedia Commons alberga contenido multimedia sobre PolinomioCommons- Polinomios, en descartes.cnice.mec.es
- Calculadora polinómica
- Operaciones con polinomios
Herramientas personales
Navegación
Imprimir/exportar
Herramientas
Otros proyectos
En otros idiomas
- Afrikaans
- العربية
- Azərbaycanca
- Беларуская (тарашкевіца)
- Български
- বাংলা
- Bosanski
- Català
- Česky
- Чӑвашла
- Cymraeg
- Dansk
- Deutsch
- Ελληνικά
- English
- Esperanto
- Eesti
- Euskara
- فارسی
- Suomi
- Français
- Frysk
- Galego
- עברית
- हिन्दी
- Magyar
- Bahasa Indonesia
- Ido
- Íslenska
- Italiano
- 日本語
- ქართული
- Қазақша
- 한국어
- Latina
- Lietuvių
- Latviešu
- മലയാളം
- Bahasa Melayu
- Nnapulitano
- Nederlands
- Norsk (bokmål)
- Polski
- Português
- Română
- Русский
- Srpskohrvatski / Српскохрватски
- සිංහල
- Simple English
- Slovenčina
- Slovenščina
- Српски / Srpski
- Svenska
- ไทย
- Türkçe
- Українська
- اردو
- Tiếng Việt
- ייִדיש
- Yorùbá
- 中文
- 粵語
- Esta página fue modificada por última vez el 29 sep 2011, a las 23:47.
- El texto está disponible bajo la Licencia Creative Commons Atribución Compartir Igual 3.0; podrían ser aplicables cláusulas adicionales. Lee los términos de uso para más información.
Wikipedia® es una marca registrada de la Fundación Wikimedia, Inc., una organización sin ánimo de lucro. - Contacto
Bloque II: Magnitudes y Números Reales
En éste bloque se estudiará las propiedades de los números reales y la manera como estos se utilizan para la resolución de problemas relativos al contexto del estudiante.
Los números reales conforman un conjunto infinito que se encuentra en relación uno a uno con los puntos de una recta infinita del plano, tal manera que a cada puntoe de dicha recta le corresponde un número. Sus propiedades fueron formalizadas a fines del siglo XIX por el matemático aleman Georg Cantor.
Los números reales conforman un conjunto infinito que se encuentra en relación uno a uno con los puntos de una recta infinita del plano, tal manera que a cada puntoe de dicha recta le corresponde un número. Sus propiedades fueron formalizadas a fines del siglo XIX por el matemático aleman Georg Cantor.
Suscribirse a:
Entradas (Atom)